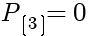Esope Blog

Soient M un ensemble de problèmes à caractère mathématique et F un sous-ensemble de M contenant les problèmes que nous appellerons faux, c'est-à-dire qui demandent de prouver que la proposition A est vraie alors qu'elle est fausse.

Théorème de la frustration : La frustration éprouvée par celui qui tente de résoudre l'ensemble M est lié de manière proportionnelle et exponentielle au nombre k d'éléments de F, modulo le nombre i de problèmes non résolus

Il faut distinguer deux cas : soit M a déjà été résolu par quelqu'un d'autre (et vous est donc soumis à titre d'épreuve par exemple), soit il ne l'est pas (et ses éléments sont alors des conjectures). Dans le deuxième cas, le théorème est à la fois trivial et semi-non-applicable : en effet, d'avoir infirmer une conjecture peut être gratifiant, mais sera en général frustrant si vous étiez fort attaché à la conjecture, et le sera certainement si vous désiriez rentrer dans l'Histoire. Nous nous intéresserons donc au premier cas.

Par hypothèse, M a été résolu par une personne autre que vous, et donc M a été formulé par cette personne. On s'attend donc à ce que cette personne ait formulé les éléments de M comme il les a trouvés, et nous demande de les trouver. Si F est un ensemble non-vide, nous pouvons supposer deux cas :

1. il s'agit d'une erreur ;
2. il s'agit d'un piège.

Le permier cas nous amène à "quelle genre d'erreur ?". Cette erreur peut être de distraction, si notamment l'élément faux peut devenir vrai en modifiant un petit nombre de sous-éléments de cet élément. Si cependant l'erreur ne peut être ainsi corrigé (cas typique d'une négation non-écrite en langage mathématique), on peut penser que l'erreur vient de la démonstration fournie par le Fermat qui nous a soumis M. Cette supposition est vite écartée si la personne qui nous a soumis M est investi d'une certaine autorité et expérience qui ne devraient pas permettre d'erreur dans les problèmes du niveau de ceux de M (ce qui signifie donc que le coefficient de proportionnalité est intrinsèque à la difficulté des problèmes).

Nous sommes donc assez rapidement amenés à penser qu'il s'agit d'un piège. Un piège sournois destiné à nous fourvoyer dans la démonstration à envisager. Si F est un singleton, cette solution est relativement acceptable. Cependant, plus k croît moins cette solution est crédible, car elle l'était déjà peu au départ. En effet, quel est l'intérêt d'un piège en mathématique ? Si vous vous lancez dans la démonstration de la proposition fausse soumise, vous aboutirez, si votre démonstration est solide, à une contradiction, et vous aurez donc réalisé un raisonnement par l'absurde sans le savoir. Il est donc permis de douter de cette solution. Si k est petit, cette solution est envisageable, mais la limite de cette solution tend vers l'absurdité quand k tend vers l'infini.

Mais alors, pourquoi F existe-t-il ? Ne sachant répondre à cette frustrante question, vous revérifiez votre démonstration. Parfois cela diminue k, souvent pas.

Quand vous remettez à la personne qui a créé M l'ensemble M' de vos solutions pour M, vous avez déjà maintes fois vérifier vos démonstrations que vous considérez donc comme solides. Peut-être même avez-vous fait vérifier vos démonstrations par un tiers. Mais ce n'est pas suffisant. Il reste un doute. Et si l'autre ne s'était pas trompé ? Ces problèmes sont terriblements frustrants ! Pourquoi n'ont-ils pas été formulés autrement ?

Le théorème est ainsi démontré. La présence de "modulo le nombre i de problèmes non résolus" est d'origine triviale : ne pas savoir résoudre un problème est frustrant si l'on est attaché au domaine du problème, ce qui est supposé être le cas ici sinon il y a longtemps que vous aurez envoyé promener l'autre qui vous a soumis M.

Ceci pour dire que je suis terriblement frustré par cet ensemble F qui contient beaucoup trop d'éléments à mon goût, comparé au nombre d'éléments de M.

Vous ne faites pas partie des chanceux qui ont un don pour la factorisation, vous connaissez toutes les méthodes de factorisation vues en classe, mais devant un polynôme vous vous retrouvez avec l'angoisse de la page blanche ?

Raisonnez méthodiquement, en suivant le schéma ci-dessous. Quand vous répondez oui à une question, passez à la ligne suivante. Quand vous répondez non ou quand la méthode que vous tentez ne fonctionne pas, passez au numéro suivant (en respectant la structure des numéros).

1. Avant tout, vérifiez bien que vous ne pouvez regrouper certains termes ensemble (s'ils ont la même partie littérale, c'est-à-dire les mêmes "lettres" avec les mêmes exposants).
2. Le polynôme a-t-il plusieurs "lettres" différentes ?
   1. Y a-t-il une des "lettres" qui apparaît dans chaque terme ?
      • Vous avez loupé une mise en évidence. Une fois celle-ci effectuée, vous devriez y voir plus clair (tant que vous y êtes, vérifiez qu'aucun chiffre ne puis être mis en évidence).
   2. Certaines "lettres" ont-elles le même exposant et le polynôme contient-il 4 termes ou moins ?
      • Dans ce cas il s'agit certainement d'un artifice de calcul ou d'une identité remarquable que vous auriez loupée (n'oubliez pas que ).
   3. Tentez une méthode d'Horner "sans chiffre" : vous choisissez une des lettres (celle qui apparaît le plus souvent, généralement partout sauf dans un terme) qui sera la variable et considérez les autres comme des coefficients. Calculez la valeur du polynôme en remplaçant la lettre que vous avez choisie par une des autres lettres (qui apparaît dans le terme indépendant).^[1]
3. Le polynôme est-il du deuxième degré ?
   • Tentez la méthode de la somme et du produit.
4. Tentez la méthode d'Horner.

Exemple

Voici un monstre :

1. Peut-on regrouper certains termes ? Non
2. Le polynôme a-t-il plusieurs "lettres" différentes ? Oui
   1. Y a-t-il une des "lettres" qui apparaît dans chaque terme ? Oui, un "x" que nous pouvons mettre en évidence, soit :

On repart donc du début avec le nouveau polynôme que nous avons obtenu, celui qui se trouve entre parenthèses :

1. Peut-on regrouper certains termes ? Non^[2]
2. Le polynôme a-t-il plusieurs "lettres" différentes ? Oui
   1. Y a-t-il une des "lettres" qui apparaît dans chaque terme ? Non^[3]
   2. Certaines "lettres" ont-elles le même exposant et le polynôme contient-il 4 termes ou moins ? Non, 8 termes, c'est mal parti pour une identité remarquable
   3. Tentons une méthode d'Horner. Nous remarquons que la lettre "x" apparaît partout sauf dans un seul terme, "3wz", qui est donc le terme indépendant. Prenons donc un des facteurs du terme indépendant, soit "3", "w" ou "z", et calculons la valeur du polynôme pour x = le facteur que nous avons choisi. Je vous laisse les calculs :-)

Nous pouvons donc factoriser le polynôme par (x - 3). On pourrait s'arrêter là et recommencer depuis l'étape n°1, mais pourquoi pas essayer les autres facteurs ?

Ca marche ! Nous pouvons donc écrire, sans oublier la mise en évidence du "x" que nous avons effectuée au début :